CONCEPTOS BASICOS SOBRE LA MUSICA 2
2– Fundamentos del sistema tonal
La música la podemos estudiar de manera horizontal, una nota detrás de otra, apareciendo la melodía, o de modo vertical, una nota melódica contra otras, pertenecientes a las melodías interpretadas conjuntamente, es el caso de la polifonía. Aparecen dos o más voces que se enfrentan verticalmente entre ellas. El estudio de la consonancia entre varias voces analizadas verticalmente o sea enfrentando sus melodías simultáneas se denomina Contrapunto.
Los acordes se producen cuando suenan dos o más notas a la vez. Estos acordes pueden ser consonantes o disonantes. Estas relaciones las estudia la Armonía y se definen a través de los intervalos. La armonía estudia la consonancia de los sonidos enfrentados verticalmente.
La armonía definida en su sentido amplio estudia las relaciones entre los sonidos tanto en su sentido melódico como armónico, en este caso diríamos que tanto el contrapunto como la armonía en su sentido restringido forman parte de ella.
Lo que se desea demostrar es que el origen de la armonía es un fenómeno puramente físico. Es necesario destacar una serie de cualidades intrínsecas que poseen los armónicos de un sonido. Su intensidad decrece a razón del cuadrado del número que los representa. Los intervalos van disminuyendo cuando va aumentando su número, o sea que cuando más separados están del sonido fundamental, más cortos son sus intervalos. Lo podemos comprobar con los quebrados que representan estos intervalos. El primero es 2/1, el segundo 3/2, el tercero 4/3, etc.
Los sonidos más armónicos son los que su relación de frecuencias es más simple, que coinciden con los primeros armónicos. En primer lugar está el que posee la relación 2/1. Sus sonidos se confunden cuando se interpretan conjuntamente. Luego se encuentra el que posee la relación 3/2.
2.1 – Sistema tonal
El sistema tonal occidental se remonta a la antigüedad griega seleccionando los tonos y sus intervalos. Desde la época del contrapunto clásico en el siglo XVI, se consideran unos determinados intervalos como consonantes y otros como disonantes.
El signo de consonancia es un elevado grado de fusión, como si las notas se parecieran, produciendo un efecto de calma y de distensión. En cambio en la disonancia se observa una fricción y acritud, con la tendencia de resolverse en una consonancia.
Se intentó explicar el sistema tonal como producido por la naturaleza, como hemos visto que decían los griegos, pero que no pudieron demostrar totalmente con su sistema basado en su estudio de las longitudes de la cuerda. Se fundamentaba en un efecto de la propia naturaleza física de los sonidos, estudiando sus armónicos. Posteriormente diversos matemáticos intentaron encontrar la solución hasta que actualmente se puede explicar a través de la acústica.
2.2 – Acústica aplicada a la música
La Acústica es la parte de la Física que estudia los sonidos. Las ondas sonoras son movimientos vibratorios que se pueden representar matemáticamente. No vamos a estudiar el razonamiento físico matemático que nos llevaría a poder calcular los distintos armónicos de un sonido fundamental, pero sí que aplicaremos sus conclusiones.
Cuando se produce una vibración el sonido no es puro, como se ha comentado anteriormente. Se producen una serie de sonidos que lo acompañan. Esta serie es conocida como serie armónica.
El Teorema de Fourier estudia las relaciones entre los armónicos de un sonido y nos da la fórmula matemática para su cálculo. La mencionamos como curiosidad a continuación pero sin demostrarla. Creemos que lo importante para la comprensión de los fundamentos de la Música son sus conclusiones.
e = A1 sen (ωt+φ1) + A2 sen (2ωt+φ2) + A3 sen (3ωt+φ3) + . . .
siendo e la elongación o sea la distancia que separa el centro de vibración y el punto movil en dicho instante de tiempo t. El resto son constantes dependientes de la fase.
La frecuencia f está relacionada con la fórmula anterior mediante la siguiente expresión:
ω = 2 π f
Sustituyendo en la fórmula de la serie de Fourier tenemos,
e = A1 sen (1*2 π f t+φ1) + A2 sen (2*2 π f t+φ2) + A3 sen (3*2 π f t+φ3) + . . .
Lo importante es comprender que todo movimiento periódico por complicado que sea, puede considerarse como la superposición de oscilaciones armónicas componentes, cuyas frecuencias serán f, 2f, 3f, 4f, …
Esto es lo que nos dice el teorema de Fourier. El primer término de la serie tendrá la frecuencia del sonido fundamental y se denomina primer armónico. El segundo término tendrá una frecuencia doble de la fundamental y será el segundo armónico y así sucesivamente. Esta fórmula nos permite calcular la frecuencia de cualquier armónico de la serie, solo multiplicando la frecuencia fundamental por el número que ocupa en la serie.
De este modo si la frecuencia fundamental es 1, la frecuencia de su quinto armónico será 5*1 = 5
Calculamos a continuación los primeros miembros de la serie para la frecuencia fundamental:
1er armónico f=1 corresponde a la frecuencia fundamental
2º armónico f=2 doble de la fundamental
3º armónico f=3 aparece un nuevo sonido
4º armónico f=4 vuelve a doblarse la fundamental
5º armónico f=5 aparece otro sonido nuevo
6º armónico f=6 doble del tercer armónico
2.3 – Series armónicas
En la siguiente figura pueden verse los 16 primeros armónicos de la nota fundamental, en este ejemplo se ha tomado la nota do.
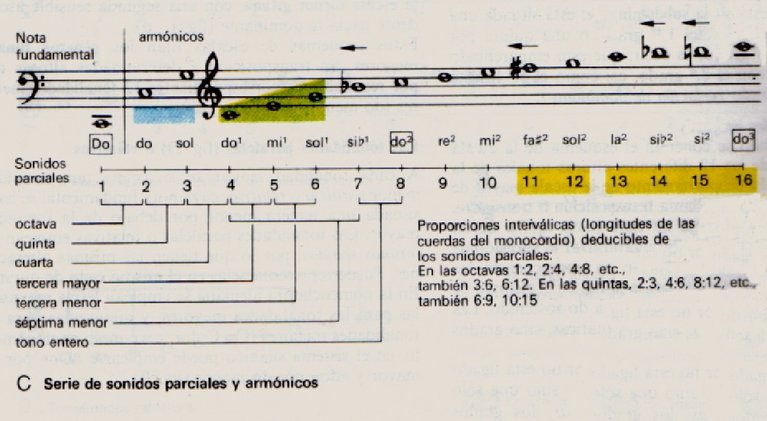
Las escalas musicales se generan a partir de los armónicos demostrándose su origen natural. Las leyes de la armonía se fundamentan en la propia naturaleza de los sonidos. Para su justificación construiremos una escala a partir de los armónicos de los sonidos que la integran.
Un sonido puro posee una frecuencia que denominaremos A, siguiendo las costumbres centroeuropeas de nombrar las notas mediante letras[1]. Este sonido genera una serie de armónicos de los cuales tomaremos los tres primeros no repetidos, por ser los que normalmente poseen más intensidad. De este modo tendremos las notas A, B y C que trasladamos al intervalo comprendido entre la frecuencia fundamental y su doble cuyo sonido es el mismo pero más agudo.
Basándonos en el estudio griego sobre la división de la cuerda vemos que sus primeras divisiones al colocarlas dentro de la escala comprendida entre la frecuencia fundamental y su doble corresponden a los 3/2 y a los 5/4 de la frecuencia fundamental. Esto coincide con lo demostrado por el Teorema de Fourier al pertenecer la primera frecuencia diferente al intervalo doble del primero y la segunda al cuádruple, con lo cual la primera la dividimos por 2 y la segunda por 4.
Con esto tenemos tres sonidos diferentes correspondientes a tres frecuencias relacionadas con la fundamental que por su intensidad son las más representativas.
Lo que no tuvieron en cuenta los griegos es que todas estas frecuencias se relacionaban e interactuaban entre ellas, como es un sistema solar en el cual la frecuencia fundamental actuaba como un astro sol y el resto como sus satélites más o menos alejados proporcionalmente.
En nuestro caso el astro sol sería la que se ha denominado como frecuencia fundamental. Es nuestro centro del sistema musical relacionando el resto de frecuencias que giran a su alrededor.
Encontramos una diferencia entre el sistema solar y el de los sonidos. En el sistema solar los diferentes elementos poseen tamaños o masas diferentes, además de su distancia al centro planetario. En el caso de los armónicos musicales la masa de cada sonido es la misma, la intensidad depende de su distancia a la frecuencia fundamental.
El resultado de todo ello es, que solo tienen importancia los primeros valores de la serie generadores de sonidos diferenciables, siendo el más importante el más cercano, en nuestro caso la frecuencia 3/2 de la fundamental.
Esta frecuencia también posee sus propios armónicos, que interfieren con el resto de la serie. Por ello deberemos calcular las nuevas frecuencias engendradas realizando el mismo cálculo que en el caso anterior de la fundamental.
Además hasta ahora solo hemos tenido en cuenta las frecuencias en sentido ascendente. Como la frecuencia fundamental es el centro de nuestro sistema planetario musical debemos calcular las frecuencias inferiores que generan la fundamental.
Para su cálculo por una parte tomaremos como nuevo centro de referencia hacia arriba el tercer armónico, el que corresponde a 3/2 y hacia abajo el que está relacionado con la fundamental también con la relación de 3/2 por debajo.
De este modo a partir de la frecuencia del tercer armónico obtenemos dos nuevas frecuencias diferentes, la cuarta situada a 3/2 de la tercera y la quinta situada a 5/4.
A partir de la fundamental en sentido decreciente aparecen dos nuevas frecuencias diferentes. La sexta relacionada a 3/2 descendentes de la fundamental y la séptima a 5/4 de la fundamental por debajo.
En este momento tenemos siete frecuencias que generan sonidos diferentes pero que deberemos colocar dentro del intervalo principal, calculándolas del siguiente modo según las reglas de cálculo matemático:
Frecuencia 1 la fundamental con relación 1/1
Frecuencia 2 3/2
Frecuencia 3 5/4
Frecuencia 4 3/2*3/2*1/2 = 9/8
Frecuencia 5 5/4*3/2 = 15/8
Frecuencia 6 2/3 + 2/3 = 4/3
Frecuencia 7 5/4*4/3 = 5/3
El paso siguiente es colocarlas ordenadamente de menor a mayor y tendremos lo que ahora podemos denominar como siete frecuencias relacionadas entre ellas.
Para fines prácticos tenemos que elegir el valor de la frecuencia fundamental. Para ello como la sociedad era preferentemente dominada por el hombre en su sentido masculino, se buscó el intervalo más cómodo para la voz humana y dentro del mismo por convención se determinó la f = 440 Hz para la sexta frecuencia de la serie ordenada. De este modo por su relación de 5/3, la fundamental se convertía en 264 Hz.
La Iglesia Católica para santificar la naturaleza y facilitar el canto litúrgico le dio un nombre a cada una de las frecuencias, que a partir de ahora llamaremos notas musicales. Los países del norte de Europa como protesta contra el poder de la Iglesia eligieron letras de la A a la G para dar nombre a las distintas notas, partiendo de la elegida como convencional de f = 440.
Como nota fundamental tomamos la nota do central, a la que damos una frecuencia de 264 Hz o sea de 264 ciclos por segundo. Tenemos siete notas diferentes que ordenadas por sus frecuencias crecientes nos darán una serie conocida como escala de do mayor.
Do, re, mi, fa, sol, la, si ,do
Es fácil calcular las relaciones que existen entre las frecuencias de las notas partiendo del do.
DO 9/8 RE 10/9 MI 16/15 FA 9/8 SOL 10/9 LA 9/8 SI 16/15 DO
264 297 330 352 356 440 495 528
A partir de estos cálculos podemos observar los intervalos o sea las distancias entre notas. Los intervalos más grandes son denominados tonos y los más cortos semitonos.
En consecuencia vemos que los semitonos MI-FA y SI-DO conservan la misma relación de 16:15. Pero el problema aparece al encontrarse dos tipos de tonos, un tono mayor con relación 9:8 y un tono menor con relación 10:9. La diferencia entre ellos es de 81:80. Esta diferencia entre los tonos mayores y menores se conoce como veremos más adelante con el nombre de coma pitagórica.
Conociendo la frecuencia de la nota fundamental, 264, podemos calcular las del resto de notas. El tercer armónico corresponde a la frecuencia 3 x 264 = 792. Dividiendo por 2 para situarla en la misma escala que la fundamental vemos que su frecuencia es 396, correspondiendo a la nota sol.
El cuarto armónico vuelve a duplicar la frecuencia de la nota do fundamental, por ello no la tenemos en cuenta. El quinto armónico tiene como frecuencia 5 x 264 = 1320 que reducida a la escala de la fundamental o sea dividiendo por 4 sería 330 Hz, correspondiendo a la nota mi.
Si realizamos las mismas operaciones tomando como fundamental la nota sol, la de frecuencia superior de las generadas anteriormente, vemos que sus dos armónicos importantes tendrán las frecuencias 3 x 396 = 1188 que reducida a su escala dividiendo por 4 dará 297 Hz, la frecuencia de la nota re y 5 x 396 = 1980 que realizando la misma reducción nos dará la frecuencia de 495 Hz o sea la de la nota si.
Siguiendo los mismos razonamientos tomando, para poder centrar la serie en el do, como fundamental la frecuencia de 352 Hz o sea la de la nota fa, observamos que sus armónicos serán 3 x 352 = 1056 que reducidos darán la frecuencia de 264 Hz, la nota do y 5 x 352 = 1760 que dividido por 4 dan 440 Hz, la frecuencia de la nota la.
[1] Una protesta de los luteranos al no aceptar las denominaciones de las notas musicales establecidas por el poder papal romano.

