CONCEPTOS BASICOS SOBRE LA MUSICA (3)
2.4 – Escalas musicales
La escala empleada anteriormente es la de do mayor. Si empezamos una nueva escala con la nota re obtendremos la escala del re mayor. Pero deberemos observar la misma relación entre tonos y semitonos. En el primer caso la relación es la siguiente:
do-re-mi-fa-sol-la-si-do
1 – 1 – ½ -1 – 1 – 1 – ½
Tono, tono, semitono, tono, tono, tono, semitono
Empezando por la nota re al aumentar un tono obtenemos la escala:
re-mi-fa-sol-la-si-do-re
1 – 1 – ½ – 1 – 1 – 1 – ½
Pero vemos que de mi a fa hay medio tono y debe haber un tono entero. Para ello deberemos aumentar medio tono obteniendo una nueva nota a la que se denomina fa sostenido. Lo mismo ocurre en el intervalo si-do. El do debe aumentarse medio tono pasando a do sostenido.
Así la tonalidad en re mayor utiliza la escala siguiente:
re-mi-fa#-sol-la-si-do#-re
Anteriormente hemos visto como a través de sus armónicos se generaban las notas de la escala de do mayor. Hagamos ahora lo mismo para la construcción de esta nueva serie, la de la escala de re mayor.
Para ello partiremos de la frecuencia de su nota fundamental, en este caso la nota re que tiene una frecuencia de 297 Hz. Siguiendo los mismos razonamientos empleados anteriormente vemos que sus dos armónicos fundamentales tendrán las frecuencias 3 x 297 = 891 que reducido nos da 445.5, una frecuencia parecida a la de la nota la y 5 x 297 = 1485 que del mismo modo nos da 371.25, una nueva frecuencia, una nueva nota que se parecerá a la del fa sostenido.
Vemos que para cumplir las leyes de la armonía esta serie necesitaría la construcción de un nuevo teclado, lo cual complica la interpretación armónica. La diferencia de frecuencias entre este nuevo la y el anterior de 440 Hz tiene una relación dada por la fracción 80/81. Por consiguiente tendríamos 440 x 81/80 = 445.5. Es lo que se conoce como veremos a continuación como coma pitagórica. Intentaremos explicar seguidamente las causas de esta aparente anomalía.
Si tomamos la frecuencia para el do central como 264 ciclos por segundo, la octava será el doble o sea 528, la quinta será 3:2 o sea 396 la frecuencia de la nota sol, la tercera mayor 5:4 o sea 330 la frecuencia de la nota mi, etc.
Si calculamos las quintas vemos que son perfectas para do, fa y sol, 528:352 FA-DO
528 / 352 = (352+176) / 352 = 1 + ½ = 3/2
Pero si lo calculamos para la nota re vemos la relación 440:297
440 / 297 = 40/27 40/27 * 81/80 = 3/2
Nos damos cuenta que debe ser aumentada por una coma 81:80, para que sea una quinta justa. Este tipo de tonalidad es llamado temperamento justo.
Esto complicaba las cosas, pues al cambiar de escala se debían de modificar las frecuencias de las notas. Para los instrumentos de teclado representaba hacer nuevos teclados según la tonalidad empleada.
El problema se presentó a mediados del siglo XVI, al aparecer la polifonía y ser necesario armonizar las voces. Se intentó igualar los intervalos entre las notas, aumentando unas con 1:2 coma o 1:4 de coma y otras disminuyéndolas. Pero al emplear las alteraciones, las notas negras del piano, resultaban diferencias, por ejemplo entre el sol sostenido y el la bemol. Las notas no eran equivalentes. No se podía intercambiar una nota por la otra sin producir disonancias.
Uno de los sistemas empleados para realizar una aproximación al sistema pitagórico, por la vía de la división de la octava en partes iguales fue el de la coma de Holder. Consiste en la división de la octava en 53 partes. Su razón numérica es igual a la raíz 53 de 2.√(53&2)
Cada tono se divide en nueve comas y todos los tonos son iguales, no existen tonos grandes y tonos pequeños. En este sistema el semitono tiene 4 comas. Sustituyendo los tonos y semitonos de la escala diatónica, compuesta por tonos y semitonos, por comas se obtiene:
9+9+4+9+9+9+4 = 53
El tono se puede dividir en dos semitonos, pero los dos semitonos resultantes no son iguales, siendo uno mayor que el otro. En este caso el mayor tendría 5 comas y el pequeño 4.
El semitono menor es llamado semitono diatónico. Es el que existe entre dos notas de diferente nombre. Por ejemplo entre las notas re y mi o entre la y si. Corresponde a 4 comas. Aparece cuando se usan las siete teclas blancas del piano.
El semitono mayor es llamado semitono cromático. Es el que existe entre dos notas de un mismo nombre, pero estando una de ellas alterada. Por ejemplo entre las notas do y do sostenido. Aparece al usar las doce notas de la escala cromática.
Con ello se deduce que cada tono contiene siempre dos semitonos de diferente naturaleza, uno diatónico y el otro cromático. Si se pasa del do al re subiendo un semitono mediante el sostenido el semitono cromático se presenta antes que el diatónico.
Si se pasa del do al re bajando la nota superior, mediante el bemol, tiene lugar lo contrario, el semitono diatónico se presenta antes del cromático. Con ello vemos que el do sostenido es diferente del re bemol, su diferencia es de una coma.
En los instrumentos de cuerda de frecuencia variable, el ejecutante se somete por su sentimiento melódico a esta diferencia. Pero en los instrumentos de sonidos fijos como el piano esto no es posible, pues sería necesario disponer de varios teclados. Por ello se emplea como veremos a continuación el acorde temperado o temperamento.
Estando los dos semitonos tan próximos uno del otro, se divide el tono en dos partes iguales, dando el mismo sonido y ejecutándose con la misma tecla.
2.5 – La Escala Temperada
Cuando en el siglo XVII los modos mayor y menor desplazaron a los modos eclesiásticos, fundamentados en las escalas clásicas griegas, apareció el problema de las comas pitagóricas.
La escala cromática de semitonos posee siete octavas con 12 quintas justas, llamadas así porque son iguales. Pero si hacemos cálculos veremos que 12 quintas justas son mayores que siete octavas.
7 octavas son 27 , o sea 128
Calculemos las quintas. Una quinta justa hemos visto que corresponde a una relación de 3:2. 12 quintas serán (3:2)12 o sea 1.512. El resultado es 129.746
La diferencia asciende a 129.746/128, aproximadamente 74/73, más o menos la cuarta parte de un semitono, la famosa coma pitagórica.
El moderno sistema tonal requiere que todos los semitonos sean iguales, para facilitar la escritura musical y simplificar los teclados. Werckmeister entre 1686 y 1687 introdujo la afinación temperada. Elimina las comas de los sistemas anteriores, al dividir matemáticamente a la octava en 12 partes iguales. Para ello renuncia a la justeza de las quintas. En este sistema doce quintas justas exceden a 7 octavas.
La escala temperada divide matemáticamente a la octava en doce distancias iguales. Al ser la frecuencia de cada octava el doble de la anterior, la distancia entre cada semitono será la raíz doceava de 2 o sea 1.0594631.
2-12 = 1,0594631 Desde DO hasta LA son 9 semitonos
1,05946319 = 1,68179
El tono de referencia se fijó en 1939 en Londres al diapasón normal LA en 440,0 Hz a 20ºC. Como correspondencia a esta frecuencia, el DO quedaba fijado a 261,63 Hz, en vez de los 256 de la afinación física.
261,63 * 1,68179 = 440,0 LA1
28 = 256 2,005448 = 261,63
DO1 261,63 Hz DO2 523,25 Hz
DO3 1046,51 Hz DO4 2093,02 Hz
Ahora podemos dar una definición más exacta de la palabra tono. El tono es una unidad de medida de los intervalos y equivale a 2 * 2-12 partes de una octava. Otra unidad relacionada es el semitono. Un tono es equivalente a dos semitonos.
En la música moderna se emplean intervalos más pequeños que el semitono. Para medirlos se emplean unidades más pequeñas, como el cent y el savart.
Una octava tiene 12 semitonos. Un cent es la unidad resultante de la división logarítmica de cada uno de los 12 semitonos en 100 partes iguales. La fórmula para el cálculo del valor en cents de cualquier relación interválica es la siguiente:
¢ Cents = log10 (relación interválica) * [1200 / log10 (2)]
Otra unidad es el savart. Un savart es la unidad resultante de la división logarítmica de una octava en 300 partes iguales.
La fórmula para el cálculo del valor en cents de cualquier relación interválica es la siguiente:
s Savarts = log10 (relación interválica) * [300 / log10 (2)]
Así una octava tiene 6 tonos, 12 semitonos, 1200 cents o 300 savarts. Un semitono serían 25 savarts o 100 cents.
En el caso de la escala sin temperar las diferencias expresadas en la unidad savart, serían de 51 savarts para los tonos mayores, como entre do y re, y de 46 savarts para los tonos menores, por ejemplo entre re y mi.
Con la escala temperada nos separamos de la rigurosa definición física de los sonidos y sus armónicos, pero las diferencias son tan pequeñas que el oído no puede apreciarlas. Con ello se simplifica mucho la interpretación musical.
El temperamento como teoría había sido expuesta por Bartolomé Ramos de Pareja en 1482, pero no se llevó a la práctica hasta principios del siglo XVIII, contando con Rameau y J. S. Bach entre sus defensores más entusiastas.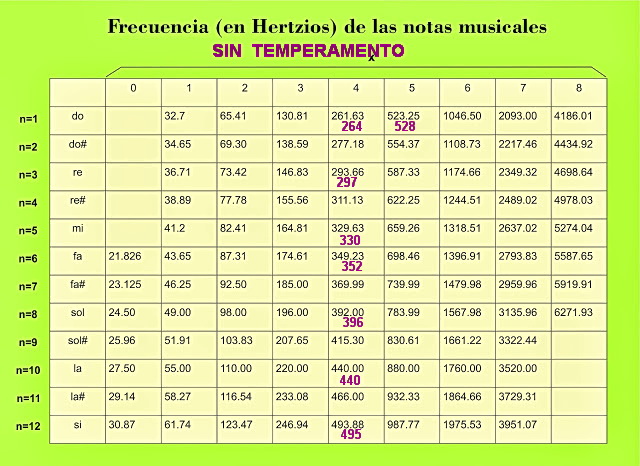
En los gráficos siguientes podemos observar las relaciones entre las notas y sus frecuencias, en la escala temperada. Si luego lo representamos en escala semilogarítmica podemos comprobar que la relación es lineal.
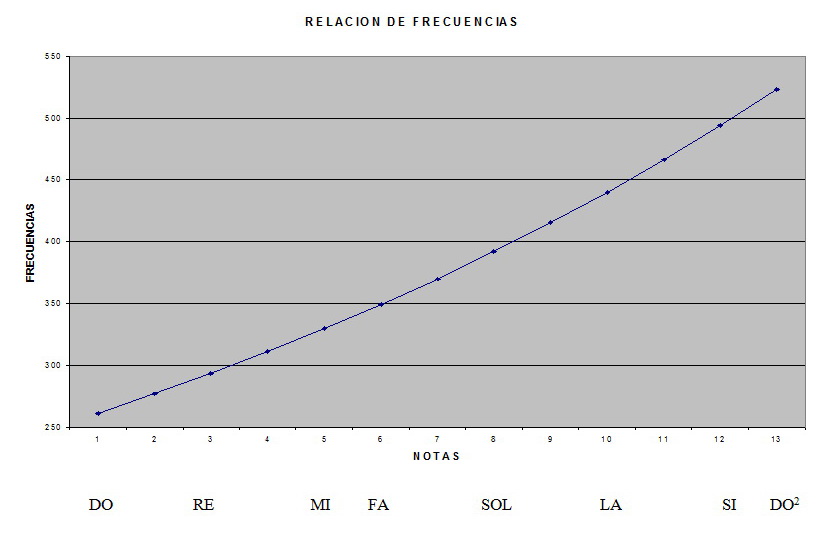
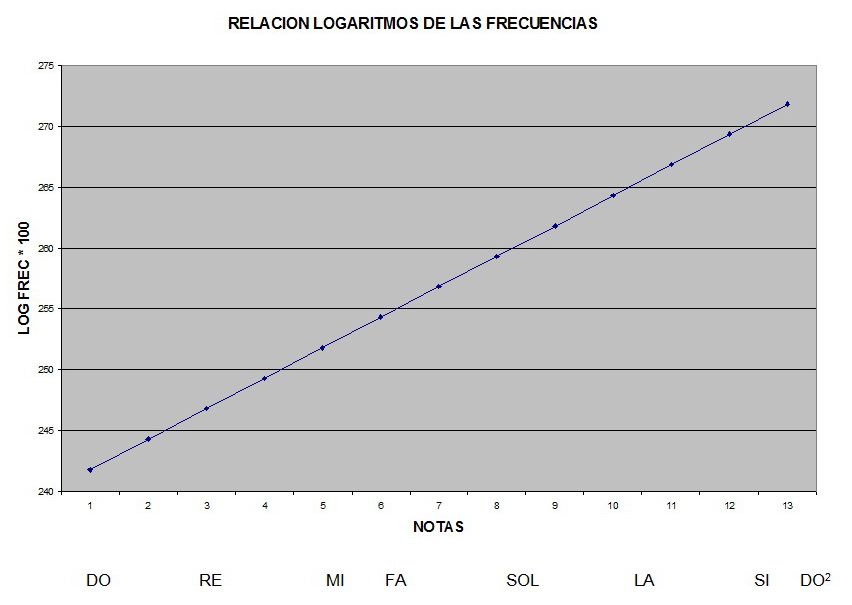
2.6 – Intervalos musicales
Los intervalos son las distancias entre dos sonidos. Son la relación entre las frecuencias de los dos sonidos o notas analizados. Pero para determinar numéricamente un intervalo no es posible hacerlo restando sus frecuencias, al estar relacionados los tonos de modo logarítmico. La determinación matemática se realiza dividiendo la frecuencia de la nota más alta por la de la más baja. Así el intervalo entre la nota sol 396 Hz y la nota do 264 Hz será 396/264 = 3/2.
La distancia diatónica determina el nombre del intervalo. De la primera nota a la segunda hay una segunda. (do-re). Asimismo serán intervalos de segunda o segundas las distancias mi-fa o re-mi. Pero existen dos tipos de segundas.
El intervalo entre la nota re 297 Hz y la nota mi 330 Hz es de 330/297 = 10/9 y es lo que se llama intervalo de segunda mayor o tono. Las notas re y mi están separadas por un tono.
El intervalo entre la nota mi 330 Hz y la nota fa 352 Hz es de 352/330 = 16/15 o sea más pequeño que el anterior. A este intervalo lo llamamos segunda menor o semitono.
En este punto debemos aclarar el significado de la palabra tono, que se usa para designar cosas diferentes. Como se ha visto, tono es la altura musical de un sonido, relacionado con la frecuencia de la vibración que lo produce. En Acústica se entiende por tono la característica de un sonido, determinada por la frecuencia del primer armónico. Los tonos empleados en música se denominan notas musicales.
Hasta ahora la cosa parece clara, pero en música el concepto es diferente. El tono es además una unidad que se emplea para la medición de los intervalos. Se llama tono al intervalo que equivale a la segunda mayor.
Comprendido este significado de la palabra tono, fácilmente se puede ver que el intervalo re-mi contiene dos pasos de semitono, es una segunda mayor. Mientras que mi-fa contiene solamente un semitono, es una segunda menor.
La distancia o intervalo entre la primera nota y la tercera se denomina tercera. La de la primera a la cuarta, cuarta, de la primera a la quinta, quinta y así sucesivamente. De este modo el intervalo entre la nota do 264 Hz y la nota sol 396 Hz será 396/264 = 3/2 correspondiendo a una quinta.
Existen intervalos que siempre son justos: primera, octava, quinta y cuarta.
Otros, como se ha visto en la segunda pueden ser mayores y menores. Estos son los de segunda, tercera, sexta y séptima. Así la tercera mayor tiene 4 pasos de semitono, la tercera menor, 3 pasos de semitono.
Además encontramos los intervalos aumentados y disminuidos. Son las alteraciones cromáticas, que se logran aumentando o disminuyendo medio tono. Así una quinta disminuida seria do–sol bemol, con cinco pasos de semitono.
Si tomamos los armónicos más cercanos, que se corresponden con los que poseen una relación de frecuencias más simples y descartamos las octavas, vemos que están en relación de 3/2 y esto corresponde a los intervalos de quinta. Aplicando esta teoría y fijando la nota do, nos aparecen cinco quintas, que se corresponden a las notas sol, re, la y mi. Con lo cual construimos una escala de cinco notas. Es la escala pentatónica, de cinco tonos, que ordenada por frecuencias nos dará la siguiente escala, desprovista de semitonos:
Do, re, mi, sol, la
Continuando el círculo de quintas obtenemos las notas si y finalmente fa. Con ello se completan las siete notas de la escala diatónica.
Estas siete notas de origen armónico natural, poseen las frecuencias siguientes:
Do 264 Hz
Re 297 Hz Diferencias con la anterior 33Hz
Mi 330 Hz Diferencias con la anterior 33Hz
Fa 352 Hz Diferencias con la anterior 22Hz
Sol 396 Hz Diferencias con la anterior 44Hz
La 440 Hz Diferencias con la anterior 44Hz
Si 495 Hz Diferencias con la anterior 55Hz
Do 528 Hz Diferencias con la anterior 33Hz
2.7 – Consonancia y disonancia
La impresión sensorial producida por dos sonidos diferentes interpretados simultáneamente, puede tener dos resultados distintos. Si los dos sonidos se combinan de modo que no puedan identificarse individualmente, hablaremos de consonancia. Los dos sonidos concuerdan, fusionándose en uno solo. Es lo que ocurre si tocamos dos notas do de octavas diferentes en un piano. Escuchamos un sonido único.
Cuando escuchamos los dos sonidos separados, pudiéndolos identificar claramente, hablaremos de disonancia. Es lo que ocurre si tocamos en el piano un sol y un la bemol simultáneamente. Encontramos una especie de oposición entre ellos.
Este fenómeno no solo ocurre cuando los sonidos se interpretan simultáneamente o sea en los acordes, sino que también cuando se interpretan uno detrás de otro o sea en forma melódica.
Las relaciones interválicas entre los sonidos forman el fundamento físico de la consonancia, o sea de las relaciones armónicas entre los sonidos. Esto viene definido por el Teorema de Tyndall, el cual establece físicamente el concepto de consonancia.
La combinación de dos sonidos es tanto más consonante, cuanto por números más simples pueda expresarse la relación de frecuencias de sus respectivas vibraciones.
Se consideran como simples los números 1, 2, 3, 4, 5, 6 y 8. El 6 por ser el resultado de 2 * 3 y el 8, 2 * 4. Los intervalos en cuyos quebrados intervienen estos números se entienden como consonantes.
Regresemos ahora a la Acústica y comprobemos los intervalos de los primeros armónicos. El primero es la nota fundamental. El segundo 2/1, es la octava. Consonancia perfecta. El tercero es 3/2. Como hemos visto representa la quinta, distancia do-sol. El acorde más consonante después de la octava. El cuarto intervalo entre los armónicos es 4/3. Es la cuarta. Luego siguen 5/4 y 6/5. Son respectivamente la tercera mayor y la tercera menor.
Las sextas mayores y menores pueden considerarse como inversiones de sus respectivas terceras, ya que no aparecen directamente en los armónicos. Así el intervalo de sexta mayor do-la tiene la relación de frecuencias 440/264 que se convierte por común múltiplos en 5/3, respetando la regla de los números simples. En el caso de sexta menor la relación sería 8/5.
Se consideran como disonantes los sonidos en cuyos intervalos aparezcan números distintos de los anteriores. Serán las segundas, séptimas, semitonos y todos los intervalos aumentados y disminuidos, o sea los que se obtienen sumándoles o restándoles un semitono.
Esta idea de consonancia es la expresada en el campo acústico. Con ello solo se pretende demostrar que el fenómeno de la consonancia tiene un fundamento físico, está fundado en la propia naturaleza del sonido.
En el campo puramente musical las explicaciones no son tan simples. Intervienen fenómenos complejos de mezclas de armónicos de los sonidos usados en el acorde. Estos armónicos pueden hacer que aumente la consonancia o por el contrario hacer el sonido más disonante. Como el timbre de los instrumentos viene reflejado por sus correspondientes armónicos, la instrumentación influye sobre la consonancia. Por ello la correcta instrumentación de una obra sinfónica, es fundamental para conseguir el grado de consonancia realmente buscado.
2.8 – Escalas diatónica y cromática
Las notas se ordenan por sus frecuencias, de menor a mayor. Es lo que se conoce como escalas musicales.
Consisten en una progresión de notas en orden ascendente, dispuestas de acuerdo a los principios de la tonalidad y de la ciencia de la armonía. Pueden ser cromáticas, compuestas por los doce sonidos o sea con todos los tonos y semitonos, o diatónicas, formadas en este caso por ocho notas dispuestas de dos modos posibles. El modo mayor que nos dará la escala mayor y el modo menor que producirá la escala menor.
La sucesión de quintas justas da como resultado la serie fa-do-sol-re-la las cuales dispuestas en escala dan do-re-fa-sol-la. Es la escala pentatónica. No tiene semitonos. Fue utilizada por los pueblos primitivos de Asia.
Escala diatónica
Nuestro sistema tonal se basa en la escala heptatónica, la escala de uso. Se forma a partir de siete quintas centradas en el re. Está compuesta por cinco tonos y dos semitonos, alternando a la distancia de dos y tres tonos enteros. Esta alternancia se denomina diatonismo. Entre el mi y el fa hay un semitono. El otro semitono se encuentra situado entre el si y el do.
Escala cromática
Esta alternancia de tonos y semitonos admitía la intercalación de más notas entre los tonos enteros. De este modo aparecen cinco tonos nuevos. Para elevar una nota un semitono se agrega un sostenido #. Para bajarla un bemol b. De este modo aparecen los cinco sostenidos do# re# fa# sol# y la#.
Téngase en cuenta que los sostenidos en la escala temperada, corresponden a los bemoles, así es lo mismo decir do sostenido que re bemol. La sucesión de los 12 semitonos se denomina escala cromática.
Do# 275 Hz
Re# 317 Hz
Fa# 367 Hz
Sol# 422 Hz
La# 475 Hz

